2023-01-08

Other posts in the series:
So encryption is a technique to secure private data so you can send it back and forth (or even store it) without anyone knowing the private data.
A thousand years ago, not many people thought that was necessary. Most had trust in a 3rd-party to secure their information in-transit, like a trusted messenger. But nowadays, trust in humans is so low, we can't really trust anyone, let alone a corporation, to handle our data and not peek through.
Encryption is so common, we consider encryption a default practice in almost all applications: when you go shopping, you assume your credit card info is not shared with the shop manager you're buying from, but beamed directly through a secure card reader to the card provider (e.g., Visa or Mastercard).
A while back, around 1978, the folks that made RSA public key encryption system talked about "homomorphism", which means that operations done after applying a function would yield the same results as applying an operation before applying a function.
In other words, assume we have two variables: plaintext1 = "bunny" and plaintext2 = "foofoo". Both are strings. An string concatenation operation like plaintext1+plaintext2 = "bunnyfoofoo" is possible in plaintexts.
But, assuming we really care about privacy and encrypt all the things, including the above plaintexts. How would we, without decrypting the strings, do a string concatenation on the encrypted versions of plaintext1 and plaintext2?
plaintext1 := "bunny"
plaintext2 := "foofoo"
key := random_bytes(n=256)
ciphertext1 = Encrypt(key, plaintext1)
ciphertext2 = Encrypt(key, plaintext2)
concat_ciphertext = concatenate(ciphertext1, ciphertext2)
// Find a function "concatenate()" that concatenates the **contents** of
// two ciphertexts without knowing the key
Why do we want to compute arbitrary operations on encrypted data? This goes back to the same trust issue we had before: we don't wanna put our trust in an organization. We wanna control our own data and have the freedom to browse the internet privately.
Computing any operation on encrypted data was not mathematically possible for a long time. You're basically asking to do operations on what essentially should be a random blob of bytes (i.e., the ciphertext of any standardized encryption algorithm).
Some people were able to come up with some schemes to do simple operations like addition and multiplication. Pascal Paillier came up with a system in the early 90s to do additions on ciphertexts. RSA, to a degree, can be homomorphic (i.e., RSA(m1 * m2) = RSA(m1) * RSA(m2)). All the schemes were known as Partial Homomorphic Encryption since they really allow you to do very basic operations, like addition or multiplication but not both. Also, they were very slow.
Then a really smart guy called Craig Gentry around 2010, possibly after watching Inception or Titanic 2 (yes, that was a thing), came up with a really smart way to do both additive and multiplicative operations.

After that, the floodgates opened and many schemes came out. And after the papers and the schemes, came the open-source libraries.
No. You cannot compute arbitrary operations on ciphertext generated from AES, chacha20-poly1305, RC4, and pretty much most of elliptic curve cryptography. It is not possible simply because the generated ciphertext belongs to a finite field under a specific very large modulo that was never intended for those operations.
FHE flipped the game a bit: we're still doing encryption, but we're doing a different sort of encryption where the resultant ciphertexts can be operated on. The new sort of encryption has its own standard made back in 2018 so it is not insecure in any way. Just different.
Let's talk about a few of those FHE schemes and libraries.
These are the names you'll hear a lot if you hang around FHE circles.
Brakerski-Fan-Vercauteren (BFV) and Brakerski-Gentry-Vaikuntanathan (BGV).
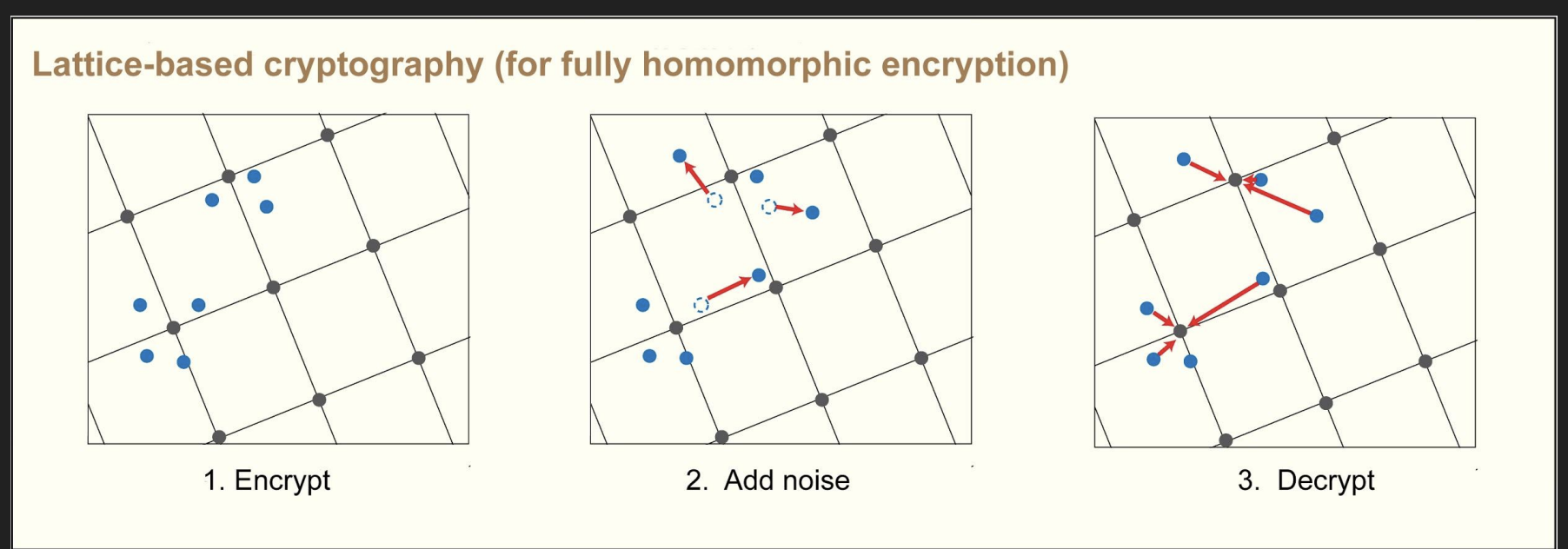
The BFV and BGV schemes both use the Ring Learning With Errors Problem (more on that later) as the main backbone for their work and both work on integers.
HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) is a homomorphic encryption (HE) method proposed by Cheon, Kim, Kim and Song (CKKS) that uses complex numbers and lattices to encrypt data. This is helpful for analytics and machine learning applications.
These are libraries that implement FHE. So far, OpenFHE (Getting Started) and Microsoft SEAL (Examples) are the easiest and best ones to use.
TFHE used to be one of the very promising voices in the field back in 2016, but a few of the creators joined a company called Zama (run by Pascal Paillier, one of the creators of the first FHE systems) and they started working on a Rust implementation for TFHE that supports more than just boolean circuits called Concrete.
Google has their own FHE transpiler that can convert C++ code to FHE circuits that can be evaluated by OpenFHE or TFHE as the "FHE Backend". It would be insanely interesting to write C++ code and have it evaluated on encrypted data. This is worth looking into.
There are a few more libraries, but TBH, just like most technologies, you'll end up knowing 1-2 libraries and know enough math to do your job. FHE is REALLY new (like 2010 new). Give it 5 more years and a winning library will emerge that everyone will use for ML and all other tech crap.